|
Programming with SoPlex Besides the main interface class SoPlex, the classes of the SoPlex library are categorized into three different types:
The main class implementing the primal and dual simplex algorithm is the class SPxSolver. The following sections are dedicated to users who want to provide own components of the simplex algorithm such as pricers, ratio tests, start basis generators or LP simplifiers to use with SoPlex's standard floating-point simplex implementation. Virtualizing the RepresentationThe primal Simplex on the columnwise representation is structurally equivalent to the dual Simplex on the rowwise representation and vice versa (see below). Hence, it is desirable to treat both cases in a very similar manner. This is supported by the programmer's interface of SoPlex which provides access methods for all internal data in two ways: one is relative to the "physical" representation of the LP in rows and columns, while the other is relative to the chosen basis representation. If e.g. a SPxPricer is written using the second type of methods only (which will generally be the case), the same code can be used for running SoPlex's simplex algorithm for both representations. We will now give two examples for this abstraction from the chosen representation. Methods
Whether the SPxBasis::Desc::Status of a variable indicates that the corresponding vector is in the basis matrix or not also depends on the chosen representation. Hence, methods Vectors and BoundsThe Simplex algorithms keeps three vectors which are associated to each basis. Two of them are required for the pricing, while the third one is needed for detecting feasibility of the basis. For all three vectors, bounds are defined. The Simplex algorithm changes the basis until all three vectors satisfy their bounds, which means that the optimal solution has been found. With each update of the basis, also the three vectors need to be updated. This is best supported by the use of VariablesThe Simplex algorithm works with two types of variables, primals and duals. The primal variables are associated with each column of an LP, whereas the dual variables are associated with each row. However, for each row a slack variable must be added to the set of primals (to represent inequalities), and a reduced cost variable must be added for each column (to represent upper or lower bounds). Note, that mathematically, one dual variable for each bound (upper and lower) should be added. However, this variable would always yield the same value and can, hence, be implemented as one. To summarize, we have a primal variable for each LP column and row (i.e., its slack) as well as a dual variable for each LP row and column (i.e., its bounds). However, not all these values need to be stored and computed, since the structure of the Simplex algorithms allow to keep them implicitly. If the SPxBasis's Status of a row or column is one of The following vectors are declared for holding the values to be computed: BoundsPrimal and dual variables are bounded (including In the dual Simplex, the basis is maintained dual feasible, while primal feasibility is improved via basis updates. However, for numerical reasons dual feasibility must be relaxed from time to time. Equivalently, primal feasibility will be relaxed to retain numerical stability in the primal Simplex algorithm. Relaxation of (dual or primal) feasibility is achieved by relaxing the bounds of primal or dual variables. However, for each type of Simplex only the corresponding bounds need to be relaxed. Hence, we define only one vector of upper and lower bound for each row and column and initialize it with primal or dual bound, depending on the Simplex type (see |



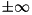 as bounds). If all primal variables are within their bounds, the Simplex basis is said to be primal feasible. Analogously, if all dual variables are within their bounds, its is called dual feasible. If a basis is both, primal and dual feasible, the optimal solution has been found.
as bounds). If all primal variables are within their bounds, the Simplex basis is said to be primal feasible. Analogously, if all dual variables are within their bounds, its is called dual feasible. If a basis is both, primal and dual feasible, the optimal solution has been found.